Proof - The Harmonic Series Diverges.

The Harmonic Series

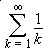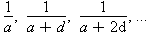The series is called the harmonic series. In general, a harmonic series is any series that can be expressed in the form . Whether or not a series diverges (grows towards infinity), or converges (grows towards a finite number) was argued for many years. Notice that when we write out the first few terms of the harmonic series that each term is getting smaller and smaller: 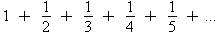. This tells us this series might converge, but does not guarantee that it converges.

The Swiss mathematician Jakob Bernoulli (1654-1705) showed, using the Leibnitz series, Sum(1/n²,n=1..∞) to demonstrate that the harmonic series diverges. This proof has the additional advantage of demonstrating a property of infinity.

Let A = 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + …

Take Leibnitz' series

1 + 1/3 + 1/6 + 1/10 + 1/15 + … = 2

and divide by 2 giving

C = 1/2 + 1/6 + 1/12 + 1/20 + 1/30 + … = 1
D = 1/6 + 1/12 + 1/20 + 1/30 + … = 1 - 1/2 = 1/2
E = 1/12 + 1/20 + 1/30 + … = 1/2 - 1/6 = 1/3
F = 1/20 + 1/30 + … = 1/3 - 1/6 = 1/4
…

We can conclude that

C + D + E + F + … = A

which means that

1 + 1/2 + 1/3 + 1/4 + … = A.

But A is also equal to

1/2 + 1/3 + 1/4 + …

which means that

A = 1 + A.

Jakob Bernouli concluded that, since the only value that can fit in the equation A = 1 + A is infinity, that A is infinity, and therefor the harmonic sequence diverges.

Other Resources