Construct the Square Root of 3

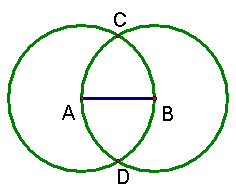
You can change the figure by clicking and dragging on points A and B. Notice that while the measure of the length of AB changes, the ratio of the length of CD to AB is always √3.

Proof

1. The length of AB is taken to be 1 by definition.
2. Because both circles are constructed with a radius of AB, they are congruent.
3. Since the segments CA and CB are both radii of congruent circles, they are congruent.
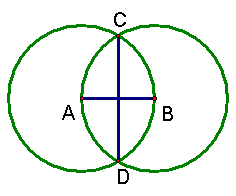
4. Since AB is perpendicular to CD (see Euclid's Proposition ??), ∠ CMB is a right angle.
5. By the Pythagorean Theorem (see Euclid's Proposition 47), BM² + CM² = BC².
6. But, since CD is unity, CM = 1/2.
7. Since CB = unity by construction, CB = 1.
8. CM² + (1/2)² = 1².
9. Since CM = 1/2 CD, (1/2 CD)² + (1/2)² = 1².
10. Simplifying give us (1/2 CD)² + 1/4 = 1.
11. 1/4 CD² = 3/4.
12. CD² = 3.
13. CD = √3, QED.