Greek Multiplication

Sorry, this page requires a Java-compatible web browser.

In the ancient Greek world, mathematics revolved around geometry. Addition consisted of placeing two line segments on the same extended line with the ends of the lines meeting. The sum was the measure of the two lines together. Even multiplication could be done geometrically!

The Sketchpad application below illustrates how this works. The geometric shape is used to solve the equality l * x = j * k, where l, j, and k are known values (independent variables) and x is unknown (dependent variable). Experiment with dragging the labeled points so that different values appear in the measures in the upper left corner. Verify with a calculator that the calculations are correct.

Greek Multiplication (Geometric Multiplication)

Here is how to construct your own multiplication problem with paper, pencil, a ruler, and a compass:

	First, determine the problem you want to solve. In the example, we are solving 3 * x = 6 * 4. Note that we are filling in the independent variables for the equations l * x = j * k. This means that l = 3, j = 6, and k = 4.
	Draw a line of length j (6 in the example).
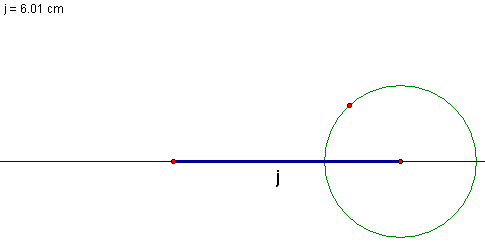
	Now we need to draw a line line perpendicular to j. To do this, we exend the line segment j, then draw a small circle with the end of j at the center. This defines two points equal distance from the endpoint of J.
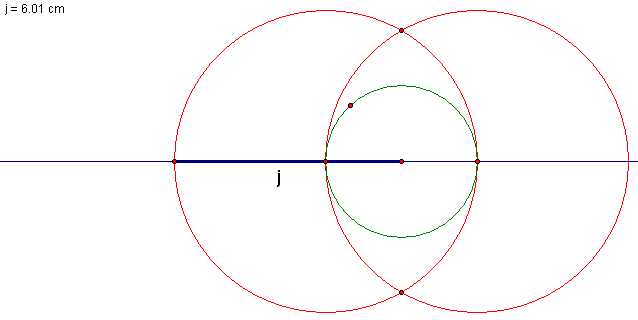
	Use the points where the circle intersects the line. Draw two more circles of the same size using the points where the first circle intercepts j as the center. The points where these two circles intercept define a line perpendicular to j which intersects the endpoint of j.
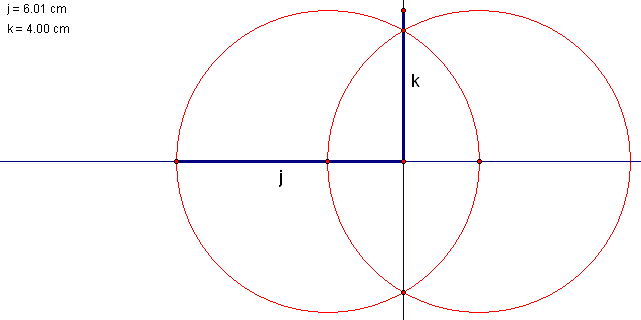
	Now we construct line segment k on the line perpendicular to j. In this example, the length of k is 4.
	Now extend line k to length l,